Base Converter
- George Fane

- Sep 9, 2019
- 4 min read
Unusually, I cannot remember why I wanted to create a Base Converter. With all my other programs, I can easily identify its intrigue: perhaps its topic was in a video by Numberphile, the Corporate Finance Institute, or Khan Academy. Nevertheless, I took on this challenge, starting off small by dealing with Bases 10 and under:
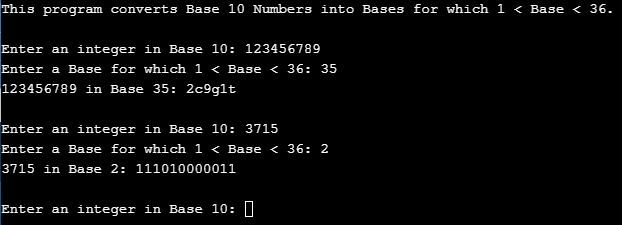
While I only have two saved versions of Base Converters, I distinctly remember making multiple, simpler programs as I progressed toward one that could convert any base to any base. I began with a Base 10 to Base <10 Converter (I'll call it Program A); much of the code is still present in the above embedded program.
Imagine an input n of 100, to be converted from Base 10 to Base 2. Using a for loop, Program A would test higher and higher powers p of the final base b (2^0, 2^1, 2^2, ...) until some power exceeded the input (2^7=128). Another for loop would divide the input by descending powers of the final base (2^6, 2^5, 2^4, ...), output that quotient as an integer q, and provide the remainder for the next iteration:
cout<<n<<" in Base "<<b<<": ";
for (p = 0; pow (b, p) < n;)
{
p++;
}
for (p--; p >= 0; p--)
{
q = n / pow (b, p);
cout << q;
a = pow (b, p);
n = n % a;
}
Excerpt A
Base 10 to Base [2, 36] Converter
I then realized that I could convert to many more bases, recalling that
a, b, c, d, e, and f are used in hexadecimal to represent digits
10, 11, 12, 13, 14, and 15. With that in mind, I upgraded my options of final bases from <10 to <37, using letters a through z for digits 10 through 35. In the place of cout << q; above in the second for loop body, I inserted:
q = n / pow (b, p);
if (q < 10)
{
cout << q;
}
else
{
cout << alphabet[q - 10];
}
a = pow (b, p);
n = n % a;
Excerpt B
where alphabet[] is initialized as:
char alphabet[26] =
{ 'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j', 'k', 'l', 'm', 'n',
'o', 'p', 'q', 'r', 's', 't', 'u', 'v', 'w', 'x', 'y', 'z' };
Excerpt C
meaning that a is in position 0 and represents 10, b is in position 1 and represents 11, and so on.
I really should have thought that through before inserting the if else code because I clearly remember the "array starts in position 0" thing tripping me up. Up to this program, I believe, I filled arrays starting in position 1, making the elements straightforward to reference, but my mom looked at one of my programs and made me start in position 0 from then on.
Through much more time than I should have needed, I realized that alphabet[q - 10] would retrieve the correct array element for a digit greater than nine. Nevertheless, I had built a program that could convert from Base 10 to any Base [2, 36].
Any Base Converter
This program meant converting an input in some initial base to Base 10, then tacking on my previous program at the end to convert from Base 10 to Base [2, 36]. If I had built this program a few weeks later, I would have included my previous program as a function, though it doesn't matter.
Converting to Base 10 entailed multiplying each digit of the inputted number by initial base to the power of position (like abc in Base 15 is a * 15 ^ 2 + b * 15 ^ 1 + c * 15 ^ 0). First I found which digit matched each letter, if there were any:
for (a = -1; alphabet[a] != in[digit]; a++)
{
out[digit] = a + 1;
Excerpt D
Then I performed the digit * base ^ position expression mentioned above:
for (a = 0, ans = 0, digit--; digit > -1; digit--, a++)
{
ans = ans + out[digit] * pow (base, a);
}
Excerpt E
I also included a few lines of code to check if the inputted number could exist in the inputted base:
for (a = -1; alphabet[a] != in[digit]; a++)
{
out[digit] = a + 1;
if (a > base)
{
error = 1;
}
}
Excerpt F
The if statement in Excerpt F comes immediately after Excerpt D. I don't know why I started the for loop with a = -1 and making out[digit] = a + 1; I could have simply made a = 0 and out[digit] = a. alphabet[-1] doesn't even exist.
I then copy and pasted my Base 10 to Base [2, 36] Converter to finish off my Any Base Converter:
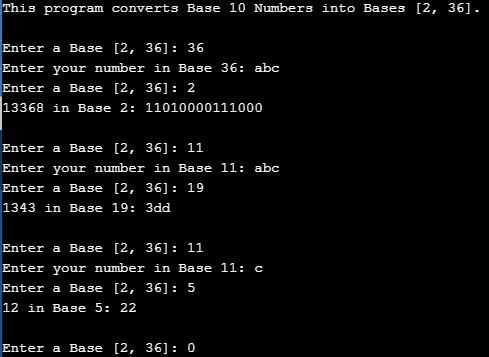
As it turns out, my check if an inputted number can exist in the inputted base does not work. I shall revamp this program right now.
Any Base Converter v2
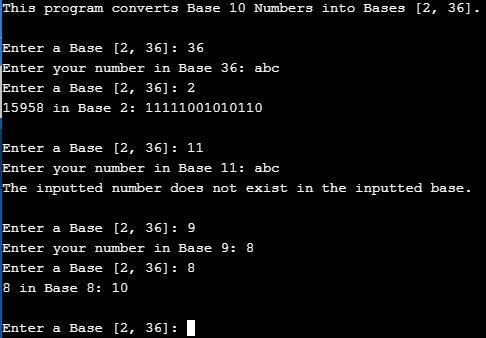
I fixed the existability checker, Excerpt F as I said I should, and another issue where 8 in Base 8 would be outputted as 8, not 10. I have finally reached a fully functioning program that can convert from any Base [2, 36] to any Base [2, 36].
Just as a side note, I have long had a fascination with codes and ciphers. I realized that Base Converters can scramble words, changing them into other letters or even numbers. This method of encryption would likely work well in low-stakes situations where the enemy, attempting to break your code, is not particularly good at math nor endowed with powerful resources like the NSA. I recall a moment in ALPS, my elementary school, when the girls were passing around supposedly uncrackable notes about a boy in my class and doubted I could read it; they simply inserted ascending letters of the alphabet after ever letter of the message.
For example,
"That boy is attractive" would combine with
"abcd efg hi jklmnopqrs" to become
"Tahbactd beofyg ihsi ajtktlrmancotpiqvres",
which would seem unreadable to most other elementary schoolers. If instead they somehow converted their message with a program similar to my Base Converter and simply gave initial and final base in a separate message beforehand, the final product would be nearly impossible for a child to crack in their head.
All in all, creating these Base Converters were great fun. While the underlying concept did not align as closely to my main interests of Finance and Number Theory, these programs offered the mathematical challenge that I appreciate so much from coding.
Thank you for reading!
George Fane

Comments