Zeta Function Approximations

The Riemann zeta function has many applications, but I wanted to focus on approximating its outputs. I had read a quite neat proof that allows the function to be expressed as an infinite product. I had never encountered infinite products before, and primes are always interesting, so I knew this task would be fun to code.

Riemann Zeta Function

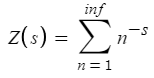
The Riemann zeta function is defined by the equation to the right (I use the letter Z in the place of the usual zeta). I never got why the input is typically expressed as the variable s (whenever I write the letter s, it looks like a 5; on the first Calc 3 test, I deliberately avoided using s as a parameter when I had two linear systems), or why the function has the exponent of negative s, which causes the output to rather unintuitively get smaller when the input gets bigger.

But those are pet peeves. Below is a program that carries out the summation:

https://onlinegdb.com/Hkbmwi_S4I

I believe this is one of the first programs that I wrote in Java outside of school. It's very simplistic code, using variables, loops, and if statements that could appear in any language. Using a scanner took some learning; I was disappointed that something like cin didn't exist in Java.

This program only effectively works for positive inputs, and only approximates at that. For negative inputs, the zeta function either diverges or has some unintuitive value assigned to the sum (perhaps most famously, -1/12 for zeta of -1: 1 + 2 + 3 + 4 + ... ).

More interestingly, though, there is a very neat process to relate the above summation to prime numbers. Leonhard Euler proved it; I'll recreate it here with Desmos.

Euler Product Formula for the Riemann Zeta Function

The proof starts by leaving fewer and fewer terms on the equation's right side, removing all multiples of 2^-s, then 3^-s, then 5^-s...

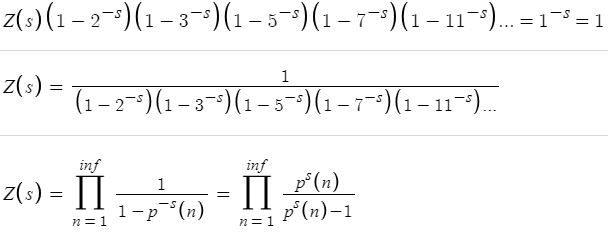
The proof does this an infinite number of times. By removing all multiples of primes to the power of -s, all terms except the first one disappear from the right side. The right side gains an infinite number of (1-prime^-s) terms multiplied together. Moving those terms back to the right side yields an expression that can be represented by an infinite product, with the nth position prime being represented by p(n). The second-to-last expression is typically the one used to describe the Euler product formula; the last expression is my simplification of it.

https://onlinegdb.com/SkJxrtrVI

Because I wrote these programs rather early on, I did not use Eratosthenes's sieve to generate my primes, even though I had already written a sieve in Python. I use an algorithm similar to PNF v4.

I've always wanted to combine the two programs to more easily check whether their results were similar. I could've copy-pasted one into the other, but I wanted to use methods to bring them together. At the time, we hadn't learned methods in AP CompSci A, but now we have. I wrote the below program right before publishing this article, as opposed to the other two which were made in the first few months of first semester.

https://onlinegdb.com/Hy6qujSVL

This program prompts the user to enter the number of terms and Zeta input, then calls the zeta function which calls the summation, eulerProduct, and error functions.

The first of the three functions is very simple, doing nearly the exact same thing as this article's first program.

The second of the three finds primes differently from the second program, calling the getPrimes function which fills and returns an ArrayList, instead of using an array. The clone function, which I just learned about today, lets me set a different ArrayList in the eulerProduct function equal to the ArrayList returned by the getPrimes function. I realize now that I could've called the getPrimes function as an eulerProduct function parameter, but I didn't think about this at the time.

The third of the three calculates error using the formula (observed - expected) / expected, which I simplified to observed / expected - 1. Only if the error has a very positive or very negative exponent when expressed in scientific notation, the error function returns the value in scientific notation.

With more terms, the error drops closer and closer to zero, as is expected. This program verifies the Euler product formula as an accurate representation of the Riemann zeta function.

---

Comparing the third program that I just created with the first two, I see how far I've come in understanding Java. Just two examples are that I can now create methods, and static ones at that (I only recently learned that they exist); and I can use ArrayLists, and iterate through them with an enhanced for loop. Even though I've only dipped a toe in the water, I can tell that programming is a never-ending journey of learning.

Thank you for reading!

George Fane