Solving and Inverting Matrices
- George Fane

- Feb 18, 2020
- 4 min read
Updated: Feb 24, 2020
Introduction
My summer internship was coming to an end; in its last week, I knew I would miss the other interns, my supervisors, and the work itself. But something new was beginning: instead of coming home after eight hours of work, eating dinner, and heading out again for a few hours of tennis, I took a different turn on the highway and headed to Schoolcraft College for my first dual-enrolled class of Linear Algebra.
I didn't know what I would learn in the class; from the name, I assumed it would just mean finding where straight lines intersected, and perhaps understanding how matrices worked. Boy, was I in for a rough ride. Despite the class's first half going by smoothly, for we had already learned a bit about determinants and vectors in Calc 2, vector spaces in the second-to-last unit hit me like a truck. But in Linear Algebra's first class, I did not yet know what I was in for. We started with the familiar task of solving linear systems, albeit with a little twist: placing the variables' coefficients into a matrix. When I got a handle on that, I wanted to write a program to solve such matrices for me. The teacher never would've let me use the program for a test, but making one would be a fun challenge and help me better remember the process to attain Reduced Row-Echelon Form.
Programs
Matrix Solver v2 - 1 Adjoined Column
After resolving to make this program, I tried imagining what I had to do. I faced the ugly possibility of embedding for loops inside for loops several layers deep, but then took a mental step back and divided the process of solving linear systems into smaller functions. To conceptualize the program otherwise seemed nigh impossible.

I definitely needed to fill the matrix, prompting the user using lines 22-29 to input entries. The prompts are in a new notation the Linear Algebra teacher showed us.
I also needed to show the matrix, writing the function to do so on lines 54-67. The output is rather plain, placing only a tab between matrix entries and a new line at the end of each row.

From there, the row operations begin. The for loop in lines 33-41 goes through the matrix from top to bottom and calls two functions, reduce() and zero(), for each row. reduce(), written in lines 69-76, divides the whole row by some number such that the leftmost nonzero number becomes one. You can see that the column alignment is messed up because the entries in the first row have many decimal digits.

Afterwards, the zero() function, written in lines 78-89, looks at the entry whose column number matches row number and through row operations, leaves only zeroes below. A different matrix is in this output.
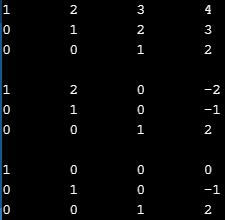
After calling those two functions for each row going downwards, the next for loop in lines 43-49 starts at the bottom row and works upwards, zeroing the column above each entry with the same row and column number.
The final matrix gives the value of each variable to the program user.
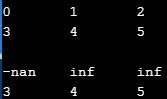
Along with the visual issues of ugly matrix display and messed-up column alignment, this program does not avoid dividing by zero:
Matrix Inverter
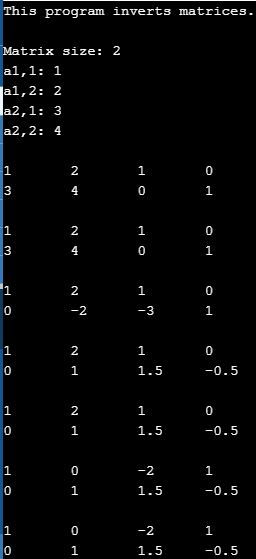
One way to invert a matrix is to adjoin the identity matrix to the right. Reducing the left side, the "original" matrix, to the identity matrix reveals the right side as the original matrix's inverted form.
This program is very similar to the first, other than the adjoinment of the identity matrix using lines 42-45. To make sure row operations still work on the entire row, for loops go up to the variable col = 2 * row (line 31), rather than only up to row + 1.
Matrix Solver v3 - General
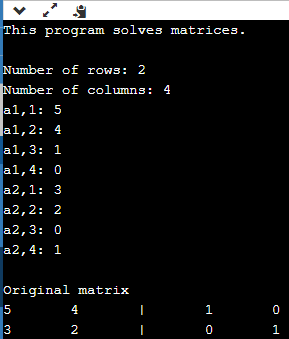
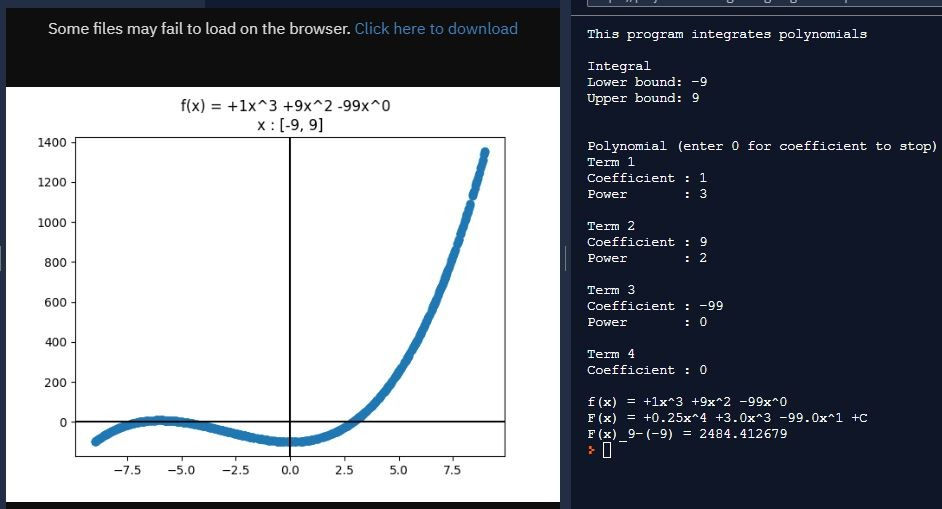
This program can solve linear systems (below), invert matrices (right), and perform other operations that I did not even know existed at the time of writing this program, like finding the transition matrix for a change of basis. Because this program is more versatile than the previous two, I more significantly tweaked this around the time of writing this article.
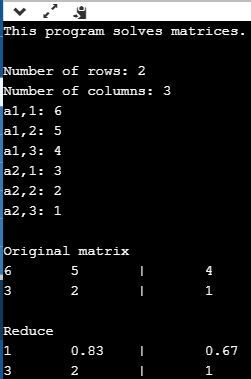
To fix alignment issues for columns due to matrix entries with lots of decimal digits, line 63 rounds entries to two decimal places.
I also added vertical lines to show adjoinment, and labels to describe each matrix operation before it happens.
To never divide by zero, I added an if statement at the start of each function to check if the divisor is zero.
*Side note (written 2/24): I actually used this program for a real-life need. I was tutoring a student in Pre-Calc over the weekend, who had to practice partial fraction decomposition. One of the steps is to find multiple variables (A, B, C, ...) that, when multiplied by expressions like x plus some constant, add up to the fraction's numerator, usually a polynomial. That required my tutee to solve a linear system; I used my Matrix Solver v3 to rapidly find A, B, and C and check his solutions when he got them. It was quite satisfying to have one of my programs be more useful than merely a coding hobby.
As always, writing these programs has shown me that existing projects can always be improved. Understanding how to fix the visual and divide-by-zero issues in Matrix Solver v2 helped me create a better product in the form of Matrix Solver v3. Additionally, existing algorithms can be tweaked and used for different purposes. I saw this before in calculating Implied Volatility for options, using the same guess-and-check method as the one in calculating Internal Rate of Return, and I see this now when my matrix-solving algorithm can solve linear systems, invert matrices, and find transition matrices.
Linear Algebra readily combines with computer science. More programs are coming that multiply matrices, project vectors, and calculate determinants.
Thank you for reading!
George Fane

Comments