Better Prime Finding Methods
- George Fane

- Nov 28, 2019
- 4 min read
Updated: Mar 2, 2020
Programming prime-finders is fun for me because it is a constant test to improve. First I divided a potential prime by all of its factors above 1, and checked whether the end quotient equaled the original potential prime (this would be the case if there were zero factors). Subsequently I checked all natural numbers below some value to test them for divisibility, and then only primes below that value. There are even better methods.
Prime Number Finder (PNF) v4
A sixth grader I tutor pulled out a few problems where she was given a number and needed to find all of its factors (the timing of the tutoring session was amusing because I had just finished my factorization program). She told me about the "Rainbow Method": starting with the lowest factors, working her way up, and drawing lines connecting "partners" of factors that multiply to yield the original number.
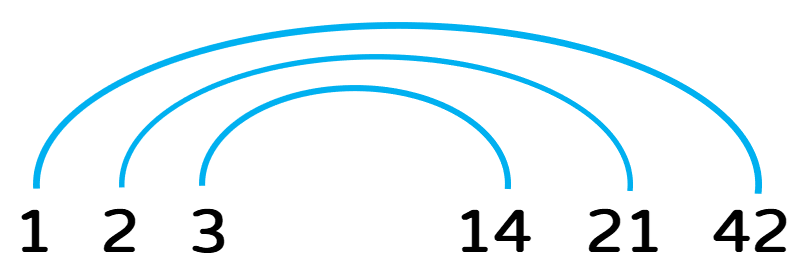
She checked every natural number below her given value for divisibility. I told her that she could just check the natural numbers at or below the square root of her value, and then find each factor's "partner". I later realized that I could use the same logic in my prime-finding programs. If there are no factors at or below some value's square root, then there are no factors anywhere.
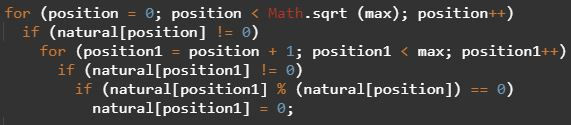
This simply meant a small tweak to a for loop condition:
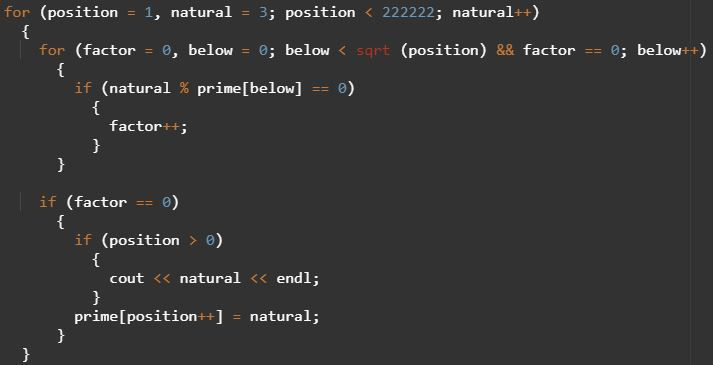

Admittedly, the latter example increments by -1 while the former increments by +1, but the essential difference I wanted to emphasize is the square root. The presence of the root makes PNF v4 much, much faster than all of my previous prime finders, enabling me to find primes above one million.
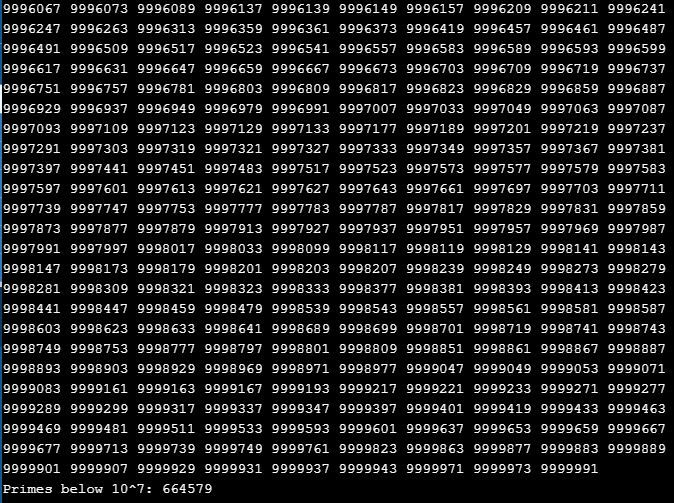
To the left is a screenshot of the last few outputs of my program. It stops at 1,299,743 because at that point my array for storing primes completely fills up, with 99,999 entries. I tried typing another 9 at the end of my array size to allocate 999,999 entries of memory, but running the program makes my online compiler unresponsive. Nevertheless, it still feels surreal to know, even a month after writing this program, that I can find all the primes up to one million.
The program is embedded below. Your computer might need to be very clutter-free to actually run this program, with nothing running in the background and no other tabs in your browser. However, after a few seconds, tens of thousands of primes should flash upon your screen.
The algorithm in PNF v4 is still not the most efficient method of finding primes, but it brought me primes of magnitudes that I had never expected to generate on my own. I used this algorithm to examine the frequency of primes, which I will discuss in a later article.
Sieve of Eratosthenes
The best is often the original. Eratosthenes, an Ancient Grecian polymath, found primes by first filling a list with all integers from 2 to some maximum he picked. The first number in the list, 2, must not have any factors other than itself and 1, so it must be prime. Going through the rest of the list, he crossed out all numbers that were divisible by 2. Jumping back to the beginning of the list, the first non-removed list entry after 2 must also be prime, because it hasn't been crossed out. That number turns out to be 3, with which Eratosthenes would repeat the process: crossing out multiples, jumping to the start, and using the next list entry as his next prime. With each cycle, Eratosthenes sieves out more and more numbers until he is left with only the primes.
This is more efficient than PNF v4's algorithm because it more quickly determines whether a number is prime. Once primes up to the square root of the list's maximum are found and used to remove their multiples, all remaining entries in the Sieve of Eratosthenes are primes. In the PNF v4 algorithm, such larger primes would be checked for divisibility by all primes up to their square root. Needing to check with lower primes at all makes PNF v4 slower.
The Sieve is not faster at checking composite numbers, though. Taking the example of, say, 49, both algorithms would check 49 against 2, 3, 5, and finally 7.
Overall, the Sieve of Eratosthenes is more efficient. Still, my Sieve program, below, is in Python. For how much I love its syntax, its speed is rather disappointing.
In roughly the amount of time it takes for PNF v4 to find the first one hundred thousand primes, my Python Sieve can only find ten thousand.

Still, writing this program was an exciting exposure to a different method of finding primes. I wrote a Sieve in Java as well, hoping to take advantage of its comparative efficiency:
My hopes proved true. My Java Sieve took about the same time to find primes under ten million as my Python Sieve for primes under ten thousand and my PNF v4 for primes under 1.3 million.
I made a few changes from my Python Sieve, resulting from the differences in Python's lists and Java's arrays. Java does not have an equivalent function for Python's list.remove, so I set composite numbers to zero:
Note: I had known for a while that if loop bodies only had one line, I didn't need curly brackets. It was only after writing the Python Sieve that I wanted to try losing brackets in a non-Python language. This leaves ungodly messes like the code screenshots above and below. Needless to say I'll keep brackets from now on.
Another change was because I couldn't print my entire list like I could in Python, forcing me to create a nicer output. I put a space between primes and jumped to the next line after every ten primes:

Java Sieve: same algorithm, different language, more efficient.
This is my first article with three languages. It's quite nice how knowledge of one language ably transfers to another; finding connections between ideas brings us more skills, more understanding, and most importantly, more interests. It has been the whole point of this website, which never would have started without chance, simultaneous thoughts of taxation and population growth. I am proud to have branched out from there, just today racking my mind for the differences in complexity between my Prime Number Finder and the Sieve of Eratosthenes.
Finding those connections in general has made me a happier person, awakening passions for math, computer science, finance, and number theory. Admittedly, the things I enjoy may not be for everyone, but, regardless, finding those connections can make all of us more balanced and driven people.
Thank you for reading and Happy Thanksgiving!
George Fane


Comments