Bond Valuation
- George Fane

- Aug 19, 2019
- 4 min read
Updated: Apr 6, 2020
Last Wednesday at my GTB internship, I met with an employee in the Finance Department. She told me about the Corporate Finance Institute, which runs a website providing educational videos, some free to watch, on various topics within finance or analysis.
Bond Present Value Calculator

I began with the first free and interesting series that I saw: Fixed Income Fundamentals, which was all about bonds. Nearly all of videos discussed theory, not calculations, although one differed.
The video explained the calculation for the present value of coupon bond. For me it was much more difficult than calculating a zero-coupon bond's present value (for which I also made a program: https://onlinegdb.com/BJ3MMstXB) which merely entailed dividing nominal value by discount rate to the power of however many years were between the present and the maturity date.
In contrast to the zero-coupon bond valuator and the three programs in the Relearning C++ article, this program actually took a while to make, probably over an hour. My first issue was learning the formula for coupon bond present value, which was completely new to me:
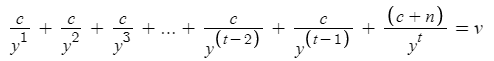
where c is Coupon Value ($), n is Nominal Value ($), y is Yield (like 1.05%), t is Term Length (years), and v is Bond Present Value.
Calculating Macaulay duration was the most difficult part of writing the code. Its calculation had essentially the same formula as Present Value, but multiplied each term by number of years after issuance and divided by Total Present Value (I named it pvt), like $102.775 in the example output above. Macaulay duration can be expressed as:
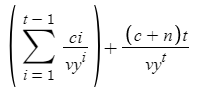
Because pvt was the output of the first for loop, I realized the calculation for total pvt (Macaulay duration) must be below that loop. I still struggled to grasp that I had to run essentially the exact same for loop over again. I didn't like that idea; it seemed inefficient. Getting past my stubbornness probably led to the longer development time of this program.
Once I had Macaulay duration, though, modified duration was easy to calculate.
Potential Improvements
Looking back to the Bond Present Value Formula, all terms except the last one are simply coupon value divided by yield to the power of an increasing exponent. I could have broken up the above formula into:
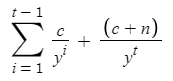
where i is years since bond issuance.
I probably should have done this. I could have simply created a for loop for the first t-1 terms and a standalone line for the t term:
for (; year <= term; year++)
{
total = total + nom * coup / 100 * pow (100 / (100 + yield), year);
}
total = total + nom * (1 + coup) / 100 * pow (100 / (100 + yield), year);
Note: coup (Coupon Value) is inputted as a whole number which, as seen in the above code, is divided by 100 and multiplied by nominal value to attain coupon value in dollars. Similarly, yield is entered as a whole number and has 100 added to it, the sum of which is divided by 100 to get, say, 1.05% if the number 5 is entered for yield. The reciprocal of yield is above.
However, I wanted to keep everything inside a single loop, so I made coup increase by 100 for the bond's maturity year:
for (; year <= term; year++)
{
if (year == term)
{
coup = coup + 100;
}
pv = nom * coup / 100 * pow (100 / (100 + yield), year);
total = total + pv;
}
I initially had issues with my outputted Macaulay duration: it was much higher than the right value. I eventually realized my coup was still above 100 by the end of the loop calculating bond value and made sure to decrease it before starting the next loop:
year = 1, coup = coup - 100;
for (; year <= term; year++)
{
if (year == term)
{
coup = coup + 100;
}
pv = nom * coup / 100 * pow (100 / (100 + yield), year);
pvt = pvt + pv / total * year;
}
Note: I unusually initialized year as 1 outside the for loop.
v2 - Array Variant
Same output, different input.
Seeing that the calculation of Macaulay duration was so difficult the first time, I made a second version of my Bond Present Value Calculator in which each term of the Bond Present Value series is stored in an array. This reduced the Macaulay duration loop into one line:
for (year = 1; year <= term; year++)
{
pvt = pvt + cou[year] / total * year;
}
The reason I didn't do this in my first version is because I forgot that arrays existed (this was especially brutal for programming a Net Present Value calculator). Mind you, Bond Valuation was one of my first few projects after the three covered in Relearning C++, so many features were still unfamiliar to me.
v3
While writing this article I realized that I could create a slightly better version of my Bond Valuation Program by tweaking my Sigma Notation for calculating Present Value and Macaulay duration.
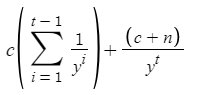
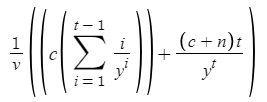
In this version, I immediately change the coupon rate and yield inputs into the values that are used in my calculations (like an input of 5 for yield immediately turns into 1.05%) and only use one for loop. I didn't even think the latter was possible; when I finished the first draft I realized that the two for loop arguments were identical and combined the interiors:
for (i = 1, v = 0, m = 0; i < t; i++)
{
v = v + pow (y, -i);
m = m + i * pow (y, -i);
}
v = c * v + (c + n) * pow (y, -i);
m = (c * m + (c + n) * i * pow (y, -i)) / v;
I calculate both series up to the t-1 term in the for loop, then, in one step, multiply that partial sum by coupon value and add term t. Compared to the original 11 lines that I needed, I now compute Present Value and Macaulay duration in only 5.
Thank you for reading,
George Fane

Comments