Factors and Prime Numbers

I watched a Numberphile video (goodness, I love that channel now) about encryption. Dr. James Grime began by reading an incredibly long number that was the product of massive primes. A computer could go through many, many numbers before finding the first factor. He then explained that the encryption process involved public and private keys, and probably other concepts, but I had already started thinking about a number factorizer program.

Factorizer v2

https://onlinegdb.com/HJMPYdlUS

Factorizer v2 - Example Output

For some inputted natural number, the program would go through all lesser natural numbers to check for factors. If the input divided by some number yielded a remainder of 0, the input was divided by that number. This would recur until the remainder became nonzero, whereupon the next natural number would be tested.

I wrote this program a while ago and do not remember the struggles of development precisely. I believe that the process of dividing the input by some number repeatedly gave me trouble, leading to a second loop nested in the first, a third in the second, and so on, all the way to a seventh nested loop. However, I created a functional solution in the end.

for (n = 2; n <= num; n++)

The only issue I have is that the above first for loop, which goes through all natural numbers above 1 to find factors, should only go through the primes, which I did not even think of until a few seconds before writing this sentence.

if (o == n)

{

cout << endl << o << " is prime!";

}

I tacked on the above statement rather flippantly because I vaguely remembered that mathematicians get excited about prime numbers. However, this led to eye-opening and exciting explorations of number theory that I will describe later.

My first version of a factorizer attempted to store every factor in an array. I remember even less of this program. However, running the program yielded a highly unusual ouput:

Factorizer (Does Not Work) - Example Output

This likely indicates that the program is outputting an array value that does not exist, like array[-1]. However, I did not think of that possibility at that time; I was so frustrated that I outputted some song lyrics with cout just to check if I was going insane.

Prime Number Finder

https://onlinegdb.com/S15ZuKgIS

Prime Number Finder - Example Output

This program expands and streamlines the tiny section of Program Factorizer v2 that finds primes. I remember that this was also a struggle to write, yet still made this more complex than necessary; I divided every natural number by all of its factors and checked at the end whether the natural number remained the same by having no factors.

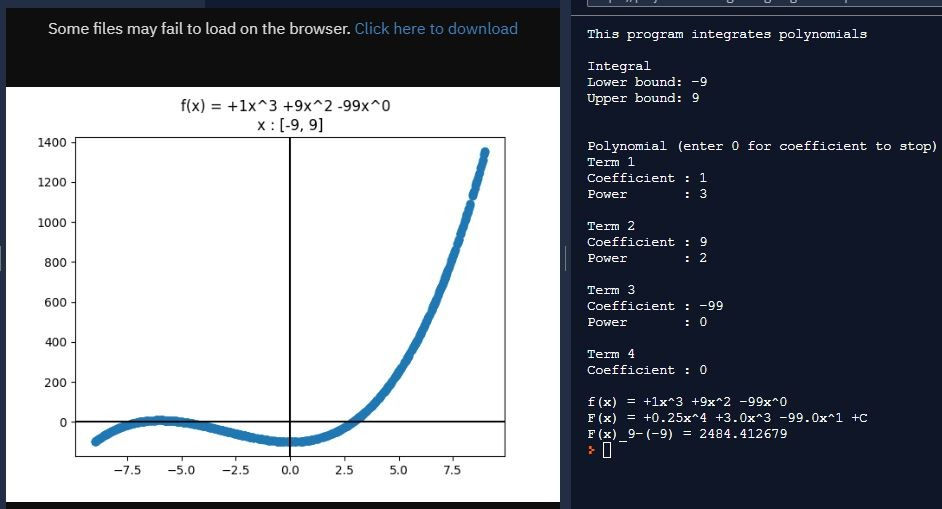
I outputted the primes as coordinates (Position, Number) because I thought I would graph them on Desmos to try finding patterns; I outputted frequency for the same reason. Later I would both graph the primes and study frequency, diving much further into number theory than I thought I ever would at the time.

---

Thank you for reading!

George Fane