Net Present Value and Internal Rate of Return
- George Fane

- Aug 27, 2019
- 6 min read
In addition to watching a video series on fixed-income securities and writing programs that perform bond valuations, I also watched a series introducing corporate finance. In the 'Capital Investment' section, the calculation for Net Present Value was shown. It intrigued me.
Formula
Spending money on any certain thing that generates cash flows, like a startup, business project, or financial instrument, has opportunity costs, decreasing the implicit value of all revenue received in the future. For example, if someone wants to use their savings to start their own company, it must eventually generate more than an average 10% a year, or else that person is better off immediately investing in, say, an ETF or passive fund of the S&P 500 (which has had 10% average annual returns since inception) for much less work.
The below image shows the formula to calculate Net Present Value, or the implicit value of all future revenues if received right now:
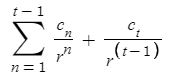
for year after inception n, annual cash flow for year after inception c_n, and discount rate r. Terminal Cash Flow c_t contains all future cash flows after a some year t-1.
Net Present Value Calculator v2
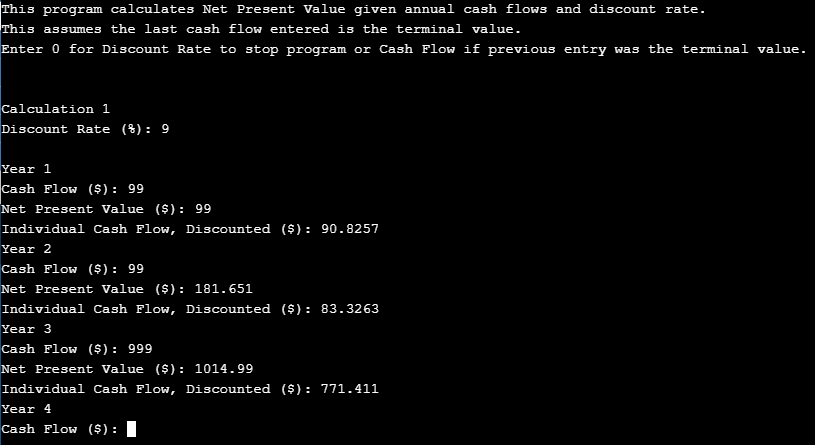
This was much more difficult to create than the Bond Valuation program, as that had constant coupons each year. In this program, I did not know which user input would be the last, terminal value and the user could input different amounts for each year's cash flow.
Each cash flow except the terminal gets divided by discount rate to the power of year after inception n. For the first cash flow, n is 1. For the second, 2. And so on. The terminal gets divided by discount rate to the power of the year after inception of the previous cash flow. For example, if 5 years of flows were entered before the terminal, both the fifth cash flow and terminal have an n of 5.
Taking over an hour (or perhaps a few), I made three versions in pursuit of a solution, getting more and more frustrated as my programs spit out inaccurate numbers. About to give up, a solution suddenly burst into my head. Realizing my second version was most compatible with the idea, I patched up v2 and sighed in contentment as I calculated Net Present Value correctly for the first time.
My solution was rather ugly but at least functional. For every cash flow entered, I acted like it was the terminal and made it have an n of n-1. Even for the first cash flow entered, I programmed n to be 0 and printed the division as Net Present Value. I then subtracted that term from the series then added it back after changing n to n, without printing. For the next cash flow entered, I again changed n to n-1, added c_2/r^(n-1), printed it, subtracted it, then added c_2/r^n, getting the partial sum ready for the next term. Ugly but functional.
NPV v2.1
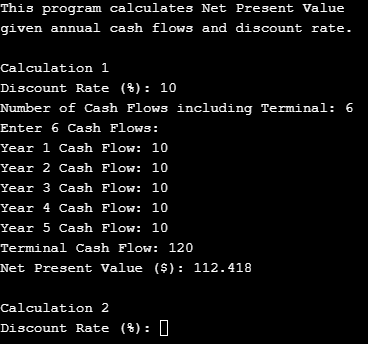
I thought I would have to use arrays; in fact, in the first draft of this article, I wrote an entire spiel about my difficult first experience with learning arrays in class. However, I realized that I could ask the user to input the number of cash flows they would input, which helps with multiple things: the program can produce nice prompts for corresponding cash flow inputs ("Year n Cash Flow: " and "Terminal Cash Flow: "), and knows which cash flow is the terminal that has a different exponent in the denominator compared to the pattern established (n++) by all previous cash flows.
Looking back at my code, I could have simplified one area, which calculates and outputs NPV for the Terminal Cash Flow starting in line 41:
npv = npv + cash / pow (1 + disc, year - 1);
}
}
cout << "Net Present Value ($): " << npv;
Instead of redefining NPV by adding the discounted Terminal Cash Flow, I should have simply outputted the sum in the first line.
Internal Rate of Return (IRR) v2

I had seen the term "Internal Rate of Return" mentioned several times before but could not figure out what it meant. I thought that it was a simple slope between each cash flow, or perhaps a moving average. When I realized that IRR (which is really discount rate) was connected with NPV, it all made sense, at least in my head. Same formula, but different inputs and outputs.
Like the calculation of implied volatility (I have an article about the Black-Scholes Model and Implied Volatility coming out soon), calculating IRR is guess and check. Cash flows and NPV, the final answer, are given by the user, but random IRR values must be used to create an NPV estimate until the estimate matches the given NPV. I now understand that IRR is usually calculated with an NPV of 0, but I did not know that tidbit at the time of my program development. Let's just say that I wanted to give more options to my user.
What is the best way to perform approximations? I know that the IRR for the user-inputted cash flows and NPV fall within some range. That range must reduce after every approximation to get more accurate, I reasoned. I thought back to how my Calc BC teacher explained convergent alternating series:
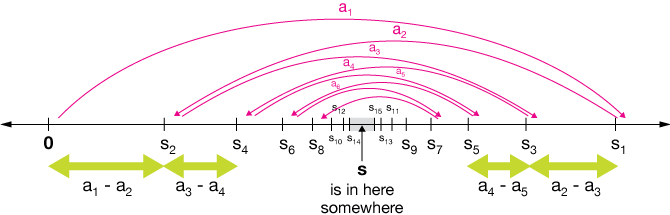
The series starts at some number (in this case 0), then has a positive term, increasing the sum to S1, then a smaller negative term, reducing the sum to S2, then a smaller positive term, and so on, until the series converges on a certain value.
I resolved to apply a similar process to my approximation code:
for (range = 1, m = 0, r = 1;
m < 99, abs (npv - net (r)) > npv / 100; m++)
{
cout << "Random IRR " << m + 1 << " (%): " << (r - 1) * 100
<< endl << "Estimated NPV: $" << net (r) << endl << endl;
if (net (r) < npv)
{
r = r - range;
}
if (net (r) > npv)
{
r = r + range;
}
range = range / 2;
}
My program starts with a random IRR value (denoted by r; I chose 0), and runs it through an NPV calculation. Depending on whether that estimate is greater or smaller than the inputted NPV, IRR adds or subtracts some value range. Either way, range halves with every new iteration of the for loop, likening the process to that convergent alternating series, making smaller and smaller jumps with each term.
Note: I made the Implied Volatility program before this IRR program, which is why, I would like to say, this IRR approximation code is much cleaner than my usual first drafts.
The IRR program in this article is not my first version; I initially tried to create upper and lower bounds, store them as the first items of an array, then update the array with new bounds every new iteration, but it didn't work and now seems complex to actually build. After seeing Version 1 fail a few times this morning, I did other things for a few hours, then started thinking again about IRR in the evening. Taking my mind away from this topic helped clear it up, enabling it to build this simple, effective program in just an hour.
Other Notes
I wrote most of this article after creating the 3 embedded programs. I was pleased to see that Program IRR v2 followed some improvement ideas that I developed wrote several hours later. In this article's NPV v2.1 section, I spoke of only outputting the sum of existing NPV and the discounted Terminal Cash Flow. In IRR v2, I returned that sum from my NPV-calculating function instead of returning a redefined total:
double
net (double r)
{
for (total = 0, n = 1; n < term; n++)
{
total = total + cash[n - 1] / pow (r, n);
}
return total + cash[n - 1] / pow (r, n - 1);
}
Furthermore, I do not hate functions as much as I used to. I initially formulated ideas for Program IRR v2 on paper and didn't want to write out my entire NPV code, so I just wrote a npv(r) inside a for loop and added a few if statements. Essentially, what I wrote down on that lined sheet of paper is mirrored in my typed code, meaning that I did choose to create a function when I gained access to a laptop.
This program is my first with more than 2 functions, counting int main(). I asked my friend if I could define variables outside of int main(), and he affirmed, at least to his knowledge of Java. I would be able to use such variables in any function, he said. It worked. I'll probably do this in the future.
This is the second of my two challenging programs about topics I learned for the Corporate Finance Institute. While CFI did not give me free access to most of its content, it was an enjoyable jumping-off point for my learning of finance. Not limited to the Black-Scholes Model and Implied Volatility, many topics will be analyzed, converted into code, and placed on this website, accompanied by my lovely, understandable, and thorough explanations.
Thank you for reading!
George Fane

Comments