Cumulative Distribution Function

I saw the Black-Scholes formula for option valuation and wanted to develop a program to calculate it, but first I must learn to code a cumulative distribution function (CDF).

Normal Distribution

Normal Distribution

This is the formula and curve for normal distribution. With arithmetic mean b of 0 and standard deviation a of 1, this is also 'standard' normal distribution, which means the total area under the curve is 1, its inflection points are at 1 and -1, and its maximum is 1/sqrt(2*pi). I will use standard normal distribution in my programs, using this formula, with the above constants substituted in:

Standard Normal Distribution (SND)

I must integrate SND from negative infinity to x to find the cumulative distribution function of x:

Note: CDF, or the integral of normal distribution, looks similar to the logistic growth curve, just as normal distribution looks similar to the derivative of logistic growth.

Integrating SND by hand was challenging to learn. I learned of one wild method in which the SND integral was set up and squared, before one of the integrals was converted into polar coordinates. However, as I learned in a 2 am Google search last night, I can integrate using a Taylor series, with which I am familiar.

e^x Approximation using Taylor Series

Rather than SNCDF, I'll start by programming the Taylor series expansion of e^x to see if this method will work, following the below equation:

Taylor series for e^x

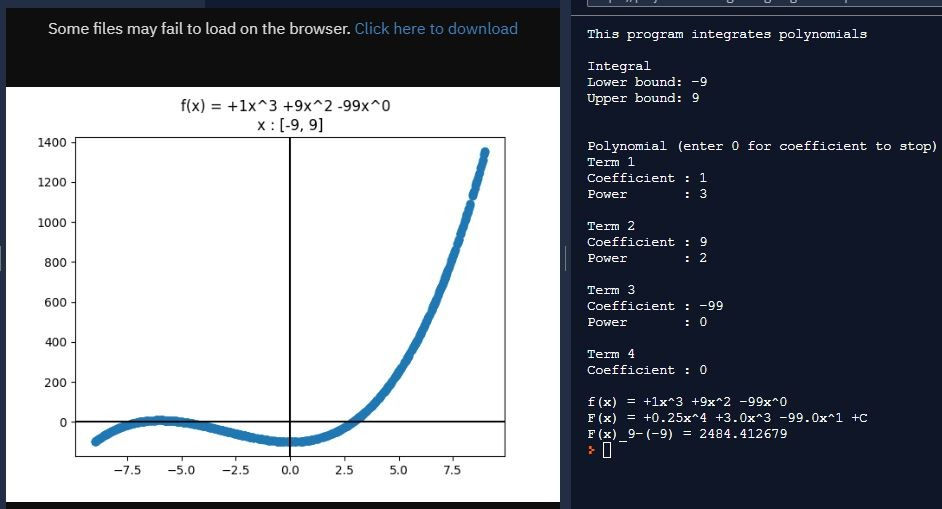
Program: https://onlinegdb.com/BJ7sVcxSB

This program was rather easy to write. I even tossed in an error calculation (observed minus expected over expected). The only hitch, and a small one at that, was creating a function for factorial. I don't normally use functions, as most things that are placed in functions can be placed inside int main(), but in this case I used one to keep the inside of my for loop short.

Standard Normal CDF Approximation using Taylor Series

Substituting the SND formula into the e^x Taylor series and integrating gives the Taylor series for the Standard Normal Cumulative Distribution Function (SNCDF):

Taylor series for SNCDF

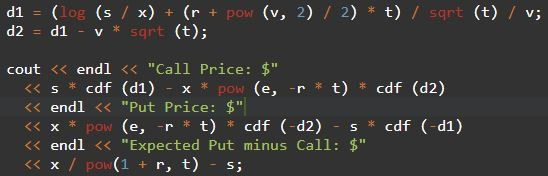
Program:

https://onlinegdb.com/SJtOh5xrH

Note: to maintain accuracy in my program, the series becomes 0 before x=-2.5 and 1 after x=2.5 because SNCDF Taylor series with finite degrees do not have near-zero slopes at the extremes:

This program had a few issues that were illogical. My approximations were more inaccurate for pow(-1/2, n) than pow(-0.5, n), even though those two expressions are the same. Additionally, the 9th degree Taylor series is more accurate than the 33rd degree Taylor series. Nevertheless, learning about the integration of normal distribution and programming a cumulative distribution function were enjoyable challenges.

---

Thank you for reading,

George Fane