Twin Prime Conjecture

It has been posited that there are an infinite number of primes that come 2 after some other prime. This pair of (n-1, n+1), where both n-1 and n+1 are prime, is called a twin prime pair.

There are other pairs of primes as well, which can be separated by any natural even numbers. However, only two other pairs are focused on strongly: cousin primes, which are 4 apart, and sexy primes, which are 6 apart.

Oddly enough, sexy prime pairs and other pairs with gaps of multiples of 6 are the most frequent pair:

*Note: The chart appears to designate all Prime Gaps that are multiples of 6 as sexy.

Update made on Sep 27

{

It is odd to me that sexy gaps are more frequent than the other kinds, but I didn't think about the cause until today. I wrote on paper the first twenty natural numbers and put a check mark next to each number if it was divisible by 2 or 3 in an effort to further streamline my prime number finders. I noticed that the "Yes"s grouped in a specific pattern:

Starting at the top, there is no "Yes" by 1, then three "Yes"s by 2 through 4, then no "Yes" by 5, then one "Yes" by 6. This pattern of 0, 3, 0, 1 repeats for every chunk of six numbers. We can see that there is never a "Yes" by numbers one more or one less than a multiple of 6 (e.g. 17 and 19, which are next to 18). While not having a "Yes" does not guarantee that a number is prime, this pattern contributes to the higher frequency of sexy gaps.

}

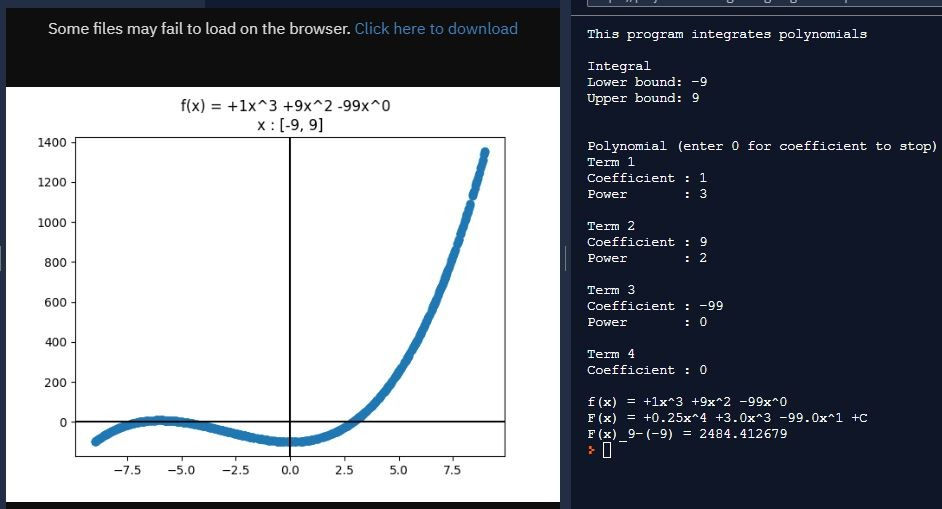
Program

https://onlinegdb.com/HyEAScTrB

I copied over my prime finder from Program Prime Number Finder v2 (I really should have pasted this is a function). Program TPC then outputs the primes (I should have pasted this as a function as well. I have certainly outputted all contents of an array before).

The output looks superficially similar to that of PNF v1:

PNF v1 - Example Output

TPC - Example Output

However, the latter has much more analysis of the outputted primes. It has the exact number of integers per prime in addition to the rounded amount, which is where PNF v1 stops. TPC's analysis also counts the number of twin, cousin, and sexy prime pairs.

Checking for individual pairs gave me trouble. I initially created all my pair checkers in this format:

if (prime[a] + 2 == prime[a + 1])

{

twin++;

}

The cousin and sexy versions had 4 and 6 respectively instead of 2 in the top line. The variable twin would be changed accordingly.

I ran this program several times, checking my total count of pairs against a website's, prime-numbers.info. I kept getting incorrect counts, eventually realizing that primes can be in cousin or sexy pairs with other primes that are not immediate neighbors. For example, 11 is not in a sexy prime pair with 13 but is in one with 17, so primes beyond next door neighbors must be checked.

Additionally, the twin prime counter was consistently wrong:

Counter Errors

It would consistently be 3 higher than the right number. Additionally, checking for cousin and sexy pairs below 100, 500, and 1000 would all work, yet doing so below 10,000 would not.

I developed this for loop as a solution to all issues:

for (minu = 1; a > 0 && minu < 4; minu++)

{

low = a - minu;

if (prime[low] + 2 == prime[a])

{

twin++;

cout << '\t' << "Twin";

}

if (prime[low] + 4 == prime[a])

{

cousin++;

cout << '\t' << "Cousin";

}

if (prime[low] + 6 == prime[a])

{

sexy++;

cout << '\t' << "Sexy";

}

}

The program would check for pairs up to 3 positions away, guaranteeing that pairs like 11 and 17 would not slip through the count, solving the issue of next-door neighbors.

In the case of the incorrect count below 10,000, I found that a number below 10,000 was in a pair with a number above 10,000, but the program did not find primes above 10,000. The code initially checked higher prime positions as possible partners (for example, 3 would check 5, 7, and 11); I changed the code so that lower positions were checked (11 would check 7, 5, and 3). This makes the pair counter accurate under 10,000.

The final issue, the consistent inaccuracy of the twin pair counter, actually stemmed from solution for the 10,000 issue. The twin pair counter would try to check lower positions, meaning that the number 2, or prime[0], would check prime[-1], prime[-2], and prime[-3] as partners. The only reason I suspected that was because I added cout << '\t' << "Twin"; to the code, showing the individual primes that were in pairs. The program would output TwinTwinTwin next to (1, 2), so I changed the for loop conditions to only check for partners for prime positions above 2's.

Through the dozens of incorrect drafts, I finally created a program that could check for prime pairs. I have seen for myself that sexy primes occur much more frequently than twin and cousin primes.

---

My table of Counter Errors contained something much more significant right next to it:

There, to the left, are the logistic growth doodles I made on a boring Spring Break morning that started this entire website. A random string of thoughts about taxation on April 3rd eventually took me on an exploration of public policy, modeling, admissions analysis, spreadsheets, finance, coding, and number theory, and I am all the more grateful.

Thank you for reading!

George Fane