Ulam Spiral
- George Fane

- Sep 23, 2019
- 4 min read
Updated: Oct 27, 2019
According to the story, Stanislaw Ulam was bored during a lecture, sometime after his work on the Manhattan Project. He began doodling: a 1 in the center of his page, then the next 8 integers in a spiral surrounding the center to make a 3 by 3 grid, then the next 16 integers in a spiral to make a 5 by 5 grid, then the next 24 integers to make a 7 by 7, and so on:

He found that primes occurred in higher frequencies within certain patterns. For example, the small Ulam spiral above contains 15 primes:
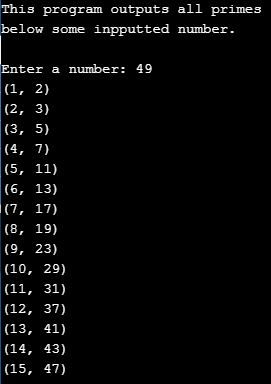
The prime frequency in this whole set is 15 / 49, or about 30.6%. However, look at the diagonal in the Ulam spiral containing the numbers 39, 19, 7, 23, and 47. That set of 5 integers contains 4 primes, yielding a prime frequency of 80%. Finding such diagonals helps to find new primes.
Program
Soon after learning about the Ulam spiral, I knew for certain that I wanted to program its output. I have not seen many cases of math being both useful and visually beautiful, but this spiral certainly fit the bill.
These spirals are easy for a human to make; all we need to do is start at the center of a page and write numbers around it. However, programs cannot start their output in the middle of the window. They print left to right, top to bottom.
Mimicking the human method of creating a spiral would mean mapping the above Ulam spiral onto these array positions:
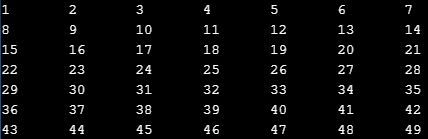
I would have had to find a way to put 37 in position 1, 49 in position 49, 1 in position 25, and everything else. The randomness stumped me; I decided to find another way.
I broke down the Ulam spiral into patterns. Imagine that the number 1 is at the center of a compass:
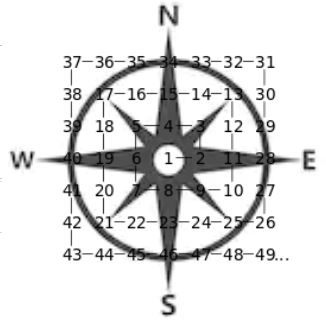
Going down the Southeast diagonal (9, 25, 49), we can see that it contains the squares of consecutive odd numbers. 9 is the first "layer" from the center, 25 is the second, and 49 is the third. We have a pattern: on the Southeast diagonal, the numbers are
((# Layer from Center) * 2 + 1) ^ 2
The Northwest diagonal appears to contain one plus the even squares, or
((# Layer from Center) * 2) ^ 2 + 1
Ulam Spiral v2 https://onlinegdb.com/ry3aQxPvr
Converting the formulas to code, we have the entire diagonal from top left to bottom right, or Northwest to Southeast:
for (r = 0, c = 0; r <= size * 2; c++, r++)
{
if (r < size)
{
ulam[r][r] = 4 * pow (size - r, 2) + 1;
down ();
}
if (r >= size)
{
ulam[r][r] = pow (2 * (r - size) + 1, 2);
up ();
}
}
Taking in the number of layers as the variable size, this for loop fills array positions (row n, column n) from (1, 1) to (2 * size - 1, 2 * size - 1) according to the aforementioned formulas.
From there, the rest of the Ulam spiral can be filled in. Looking at the Northwest diagonal first, each number moving down is one more than the number above it, while each number moving right is one less than the the number left of it. The function down(), in the first if statement, handles this task:
void
down ()
{
for (n = 1; n <= (size - r) * 2; n++)
{
ulam[r + n][c] = ulam[r][c] + n;
ulam[r][c + n] = ulam[r][c] - n;
}
}
The for loop body performs what I just said, of filling in numbers down the rows and left through the columns from the Northwest diagonal. I made this function so that each new number would not need to refer to the number right next to it; it need only refer to the diagonal. If a new number is 3 away from the diagonal (n), then it will be 3 more if 3 rows down or 3 less if 3 columns right.
The for loop condition makes sure that the filling-in of numbers stops at the right place.
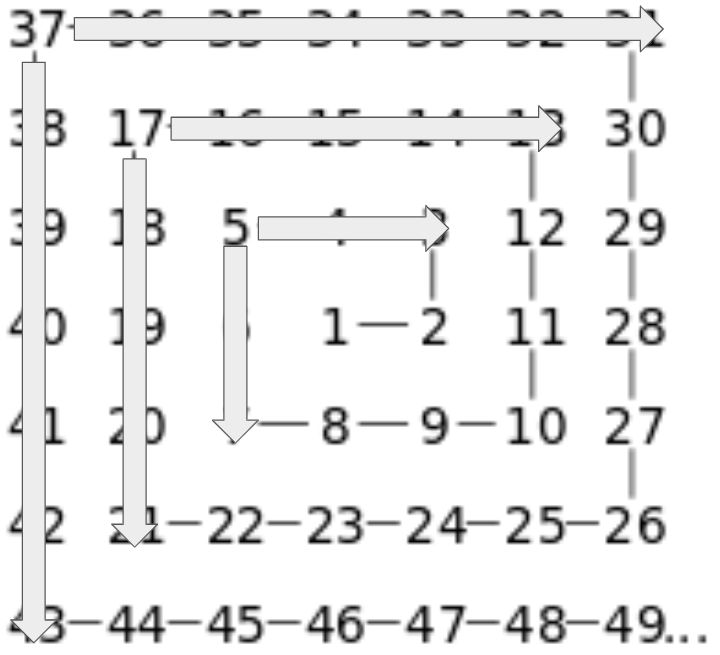
Otherwise, the for loop body would operate all the way down and all the way right. For example, the number 44 would show up as 22, being 5 rows down from 17 on the Northwest diagonal. 45 would show up as 9, being 4 rows down from 9 on the diagonal.
Half of the up() function in the second if statement works similarly:
ulam[r][c - n] = ulam[r][c] - n;
which results in:
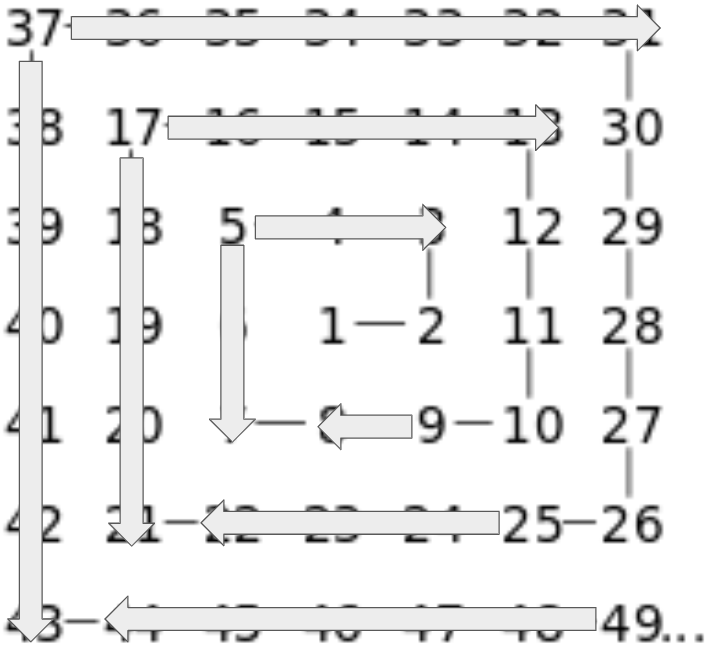
Unfortunately, we cannot work up from the Southeast diagonal to handle the last quadrant of my Ulam spiral. Moving upwards, 9 jumps to 2, 25 jumps to 10, and 49 jumps to 26.
Fortunately, our Northeast diagonal is already filled in by this point in the program, so we can work down from there:
ulam[2 * size - r + n][c] = ulam[2 * size - r][c] - n;
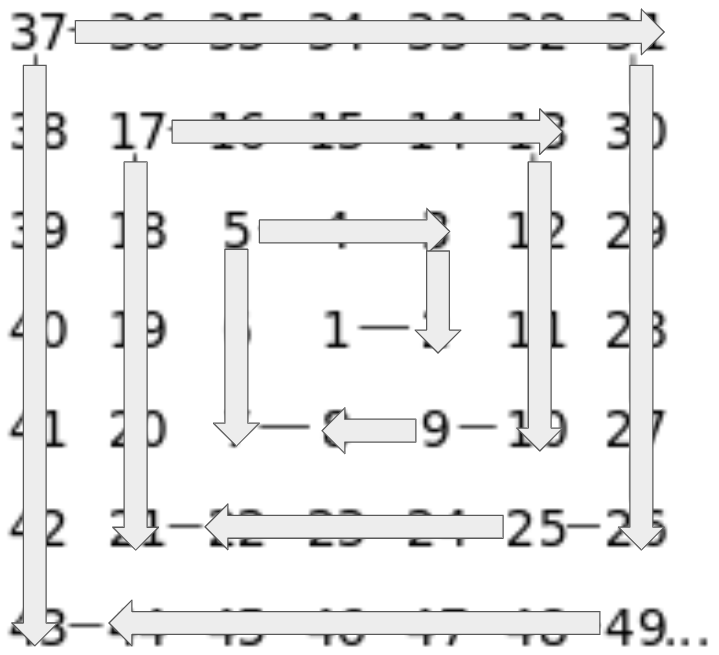
Starting with just the diagonal from top left to bottom right, I can fill in an entire Ulam spiral.
The final, heretofore unmentioned parts of the program are largely display tools. Using the log10 trick from the Goldbach Conjecture Program spaces out the numbers nicely:
l = log10 (ulam[r][c]);
for (n = 0; n <= 2 - l; n++)
{
cout << " ";
}
and copying over a Prime Number Checker leaves blanks where there are primes:
void
prime ()
{
for (factors = 0, plu = 2; plu < ulam[r][c]; plu++)
{
if (ulam[r][c] % plu == 0)
{
factors++;
}
}
if (factors == 0)
{
for (n = 0; n < 4; n++)
{
cout << " ";
}
}
}
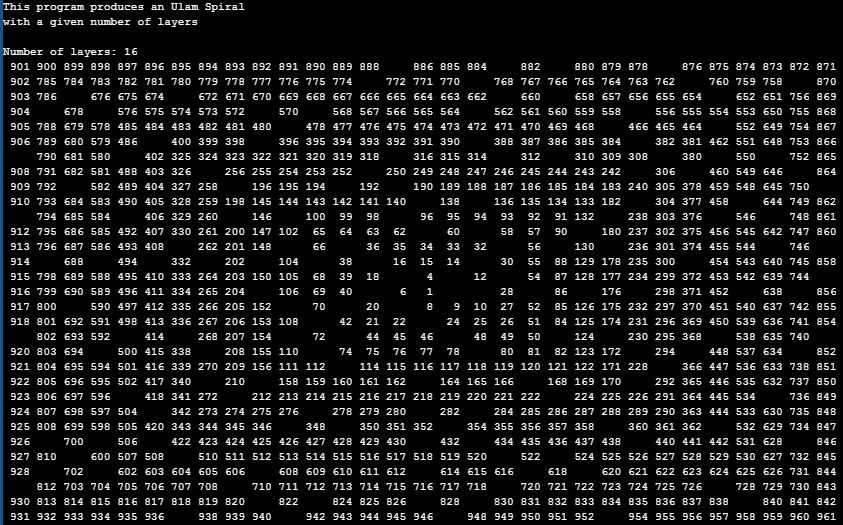

What a beauty!
Thank you for reading!
George Fane

Comments